「Luogu P2532」[AHOI2012]树屋阶梯

发表于 |
字数统计: 562 | 阅读时长 ≈ 3

引言

NOIP rp++!

链接

Luogu P2532

题解

考虑$f_i$表示搭$i$层高的阶梯的方案数，$g_{i,j}$表示最左下角的钢材上面有$i$层高，右边有$j$层高的方案数，那么如图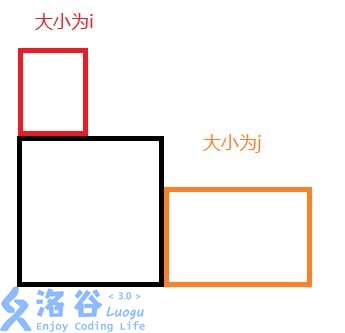

$f_n=\sum^{n-1}_{i=1}g_{i,j}$
而
$i+j=n$且$g_{i,j}=f_if_j$
$\therefore f_n=\sum^{n-1}_{i=1}f_if_{n-i}$
显然是卡特兰的递推式，所以就可以用卡特兰数求，但是要用高精度……

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
#include<bits/stdc++.h>
using namespace std;
typedef int ll;
const ll MAXN=2e4+51; 
struct BigInt{
    ll digit;
    ll num[MAXN];
    BigInt()
    {
        memset(num,0,sizeof(num));
    }
    inline void operator =(ll x)
    {
        while(x)
        {
            num[digit++]=x%10000,x/=10000;
        } 
    }
    inline void op()
    {
        printf("%d",num[digit-1]);
        for(register int i=digit-2;i>=0;i--)
        {
            if(!num[i])
            {
                printf("0000");
                continue;
            }
            ll rest=3-(ll)(log10(num[i]));
            for(register int j=rest;j;j--)
            {
                putchar('0');
            }
            printf("%d",num[i]);
        }
    }
    inline bool operator >(const BigInt &rhs)const
    {
        if(digit!=rhs.digit)
        {
            return digit>rhs.digit;
        }
        for(register int i=digit-1;i>=0;i--)
        {
            if(num[i]!=rhs.num[i])
            {
                return num[i]>rhs.num[i];
            }
        }
        return 0;
    }
}; 
ll num;
BigInt res;
inline ll read()
{
    register ll num=0,neg=1;
    register char ch=getchar();
    while(!isdigit(ch)&&ch!='-')
    {
        ch=getchar();
    }
    if(ch=='-')
    {
        neg=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        num=(num<<3)+(num<<1)+(ch-'0');
        ch=getchar();
    }
    return num*neg;
}
inline BigInt operator +(BigInt x,BigInt y)
{
    BigInt res;
    ll carry=0;
    res.digit=max(x.digit,y.digit)+1;
    for(register int i=0;i<=res.digit;i++)
    {
        res.num[i]=x.num[i]+y.num[i]+carry;
        carry=res.num[i]/10000,res.num[i]%=10000;
    }
    if(!res.num[res.digit-1])
    {
        res.digit--;
    }
    return res;
}
inline BigInt operator *(BigInt x,ll y)
{
    BigInt res;
    ll carry=0;
    res.digit=x.digit+1;
    for(register int i=0;i<=res.digit;i++)
    {
        res.num[i]=x.num[i]*y+carry;
        carry=res.num[i]/10000,res.num[i]%=10000;
    }
    if(!res.num[res.digit-1])
    {
        res.digit--;
    }
    return res;
}
inline BigInt operator /(BigInt x,ll y)
{
    BigInt res;
    ll cur=0;
    res.digit=x.digit;
    for(register int i=x.digit-1;i>=0;i--)
    {
        cur=cur*10000+x.num[i];
        if(cur>=y)
        {
            res.num[i]=cur/y,cur%=y;
        }
    }
    if(!res.num[res.digit-1])
    {
        res.digit--;
    }
    return res;
}
int main()
{
    num=read();
    res=1;
    for(register int i=1;i<=2*num;i++)
    {
        res=res*i;
    }
    res=res/(num+1);
    for(register int i=1;i<=num;i++)
    {
        res=res/i/i;
    }
    res.op();
}