学习笔记·平衡树

发表于 |
字数统计: 663 | 阅读时长 ≈ 3

平衡树是一种使用较为广泛的数据结构，代码比较长。

Splay

Splay最主要的一点是它能反转区间，而Treap以及替罪羊不能，这也是为什么它作为Link Cut Tree的辅助树。

框架

首先需要写一个这样的程序框架：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
#define DEBUG printf("In function %s, line %d\n",__FUNCTION__,__LINE__)
using namespace std;
typedef int ll;
const ll MAXN=2e5+51;
inline ll read()
{
    register ll num=0,neg=1;
    register char ch=getchar();
    while(!isdigit(ch)&&ch!='-')
    {
        ch=getchar();
    }
    if(ch=='-')
    {
        neg=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        num=(num<<3)+(num<<1)+(ch-'0');
        ch=getchar();
    }
    return num*neg;
}
ll cnt,qcnt,l,r;
namespace Splay{
    struct Node{
        ll fa,val,size,tag;
        ll ch[2];
    };
    struct Splay{
    	ll tot,root;
        Node nd[MAXN];
        //Code goes here
    };
}

以下代码片段全部接在注释处。

基本操作

首先是$update$，用于更新节点的$size$。
既然写过线段树，那么这个操作应该不难。

1
2
3
4
inline void update(ll x)
{
nd[x].size=nd[nd[x].ch[0]].size+nd[nd[x].ch[1]].size+1;
}

接下来是$id$，用于判断一个节点是它的父亲的哪一个孩子。
这个很简单，只需要几行代码。

1
2
3
4
inline bool id(ll x)
{
    return nd[nd[x].fa].ch[1]==x;
}

下一个是$connect$，用于建立新的父子关系，这个也不难。

1
2
3
4
inline void connect(ll x,ll fa,ll dir)
{
    nd[x].fa=fa,nd[fa].ch[dir]=x;
}

关键操作

以下两个操作是旋转操作，很关键，而且不好调。
首先是$rotate$，用于平衡旋转。
举个栗子，这是原来的平衡树。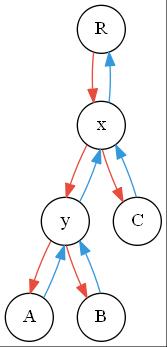

其中蓝色指向父亲，红色指向儿子。
调用$rotate(y)$之后，平衡树就变成这个样子了：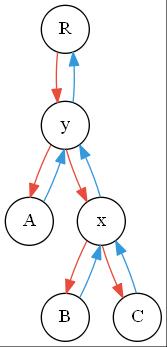

由于之前$connect$的实现，这个就变得不难了，因为旋转依次要改变$3$对父子关系。
第一对，对照第二幅图可以发现，可以直接在$y$与$R$建立关系，就像这样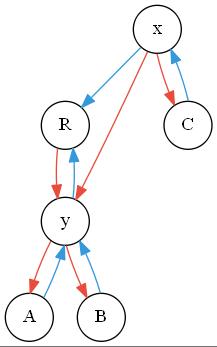

第二对，在$B$与$x$之间建立父子关系，然后就变成了这个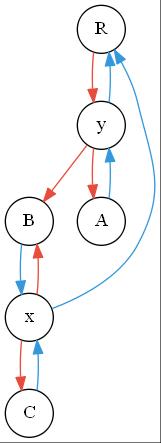

最后，在$x$与$y$建立父子关系就大功告成啦qwq。
所以，上代码

1
2
3
4
5
6
7
8
inline void rotate(ll x)
{
    ll fa=nd[x].fa,gfa=nd[fa].fa,dir=id(x);
    connect(x,gfa,id(fa));
    connect(nd[x].ch[dir^1],fa,dir);
    connect(fa,x,dir^1);
    update(fa),update(x);
}

还有一个是$splay$，这个尽管代码不长，但是很难调。
我不推荐直接上旋，因为这样可能会很慢。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
inline void splay(ll cur,ll target)
{
    while(nd[cur].fa!=target)
    {
        ll fa=nd[cur].fa,gfa=nd[fa].fa;
        if(gfa!=target)
        {
            rotate(id(cur)^id(fa)?cur:fa);
        }
        rotate(cur);
    }
    if(!target)
    {
        root=cur;
    }
}

一些特例