「CodeForces 848E」Days of Floral Colours

发表于 |
字数统计: 3k | 阅读时长 ≈ 14

我的翻译解释的挺详细的啦qwq（主要是这题不好写简要题面，建议对着我的翻译看）

$\texttt{Data Range:}3\leq n\leq 5\times 10^4$

链接

Luogu

vjudge

题解

我 tm 终于上 $\texttt{Expert}$ 啦qwq （每日发牢骚）

非常考验你的生成函数功底呢（我的生成函数功底不好，并且我的画功也不行，一个圆都画不好）。

详细的讲解一下这个分治 $\texttt{FFT}$ 做法，绝对不是对官方题解的翻译！（图是蒯的）

由对称性可知，我们可以把一个环拆成两个半环，某一个半环的连线方式可以另一个半环的连线方式唯一确定的。

然后规定 $f_{0,i}$ 表示某两朵花与它们对面的花连起来，中间夹着 $i$ 朵花的答案，这样的图形我们暂且称作长度为 $i$ 的段。长度为 $7$ 的段长这样：

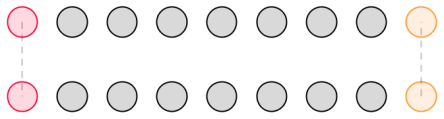
当然，后面还可能会出现连续段这个名词，意思与翻译一样。

对于长度为 $i$ 的段，我们将灰色部分（灰色的花朵）编号如下：

上面那些从左到右编号为 $0,1,\cdots i-1$，下面那些从左到右编号为 $0^\prime,1^\prime,\cdots (i-1)^\prime$。

然后我们用人类智慧可以看出各种各样的合法连线方式都是由四种连线方式组成的，如下图（图是蒯的，我觉得 $\texttt{s}$$\texttt{hadowice1984}$ 比我画的好多了）

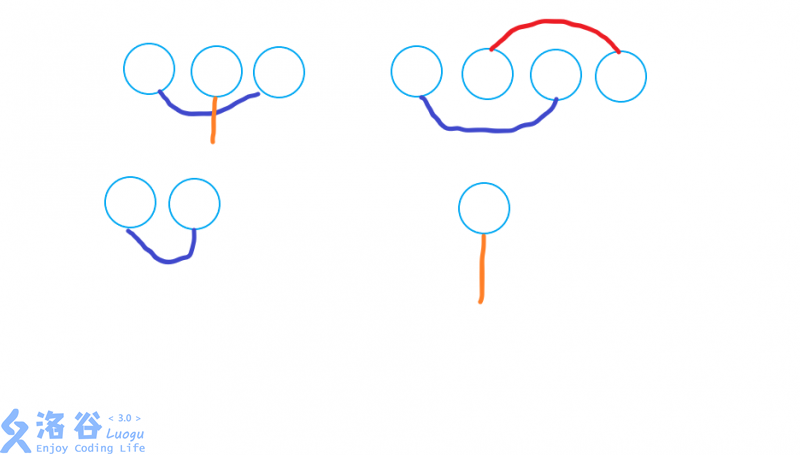
我们把这些方式从上到下，从左到右编号为 $1,2,3,4$（也就是说，左上角是 $1$，右上角是 $2$，以此类推）

准备工作做好了之后，接下来是正式解题时间啦qwq，我们需要对某个 $n$ 来求出答案。这里分两个大类讨论。

  • 情况 $1$，不存在 $p(0\leq p\leq n-1)$ 使得 $p$ 与 $p^\prime$ 相连。

    这个大类还是比较好讨论的。

    设 $g_i$ 为长度为 $i$ 的段灰色部分的上部使用方式 $2,3$ 拼接起来（其实也是整个灰色部分）的方法数，我们可以发现是个背包（实质是斐波那契，$g_{2i}=Fib_i$），有两种物品，花费为 $2$ 和 $4$，可以简单写出方程：

    然后我们发现这一个大类所带来的贡献为 $n^2g_n$。（因为灰色部分的上部和下部均为长度为 $n$ 的连续段）

  • 情况 $2$，存在至少一个 $p(0\leq p\leq n-1)$ 使得 $p$ 与 $p^\prime$ 相连。

    我们钦定最小的那个 $p$ 为 $j$（这个大类的讨论过程中所有给出的图中 $j$ 的位置由绿色标出）

    这里要分两个小类，因为方式 $1$ 的左边和右边的两朵花属于两个不同的连续段。

    • 情况 $2.1$，$j$ 这个位置的连线方式为 $4$（也就是直接连到对面的点）。

      这种情况如下图：

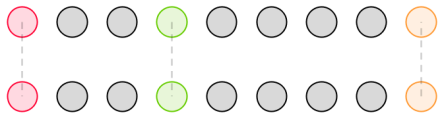
      我们会发现由于 $j$ 是第一个与对面的点连起来的位置，所以 $j$ 左边的一段变成了情况 $1$，答案为 $j^2g_j$，但是右边又回归到了原问题，所以右边的答案为 $f_{0,n-j-1}$。

      所以，由乘法原理，可以算出贡献为 $j^2g_jf_{0,n-j-1}$。

    • 情况 $2.2$，$j$ 这个位置的连线方式为 $1$（敲黑板，划重点啦qwq）。

      还是先给个图吧：

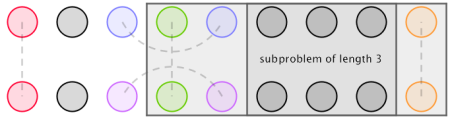
      $j$ 左边的子问题一如既往地为情况 $1$，但是规模变成了 $j-1$，因为 $j-1$ 已经连上去了。

      右边我们变成新的一个子问题。看起来像一个段，但是左边变成了两个已配对的花。这样的话，左边那个已经配对的花与灰色部分为连续段，要计入答案。如果中间灰色部分长度为 $i$，我们把它记为 $f_{1,i}$。

      这样我们就可以表示这个的答案了，为 $(j+1)^2g_{j}f_{1,i-j-3}$。（为了不出现一些奇奇怪怪的锅，这里下标做了调整）

至此，我们的讨论已经完毕啦，现在我们来将结果整合一下，有

同理，$f_{1,n}$ 类推，只不过有

现在我们解决了段的问题。接下来是时候来解决真正的问题啦qwq！

现在，由于这是个环，所以我们钦定一朵与它对面的花连在一起的花。这朵花我们编号为 $1$，然后顺时针编号为 $2,3,\cdots,2n$。容易发现，$p(1\leq p\leq n)$对面的那朵花是 $p+n$。

但是要形成一个段，还要一朵与对面的花连起来的花。这里我们钦定最小的 $p(2\leq p\leq n)$ 使得 $p$ 与 $p+n$ 有边连接的为 $i$。当 $n=9$ 且 $i=5$ 时，如下图：

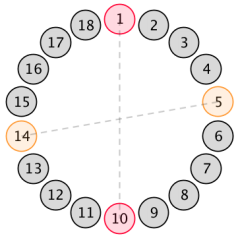
然后我们可能不清楚 $1\sim i$ 之间是否有无距离为 $2$ 的两朵花连起来（如果不考虑的话我们会算漏），然后我们又开始讨论。

讨论来，讨论去，最终发现我们出现了新的一个子问题，一个长度为 $n+2$ 的段，位置 $0$ 和位置 $n+1$ 已经配好对了，我们把它记做 $f_{2,n}$。

有了上面的讨论过程，相信你也对推 $f_{2,n}$ 的方法不陌生了吧qwq，这里就直接给出答案。

接着，我们来计算答案。这里又是一个大的分类讨论。

如果只有一朵花连到对面的话，那么是两个连续段，长度为 $n-1$。

如果这朵花的连线方式为 $1$ 的话，那么答案为 $g_{n-3}(n-1)^2$，否则为 $g_{n-1}(n-1)^2$。

否则，那么存在更多的花连到对面。然后我们可以考虑钦定一个点 $1$ 来算。

如果 $1$ 和 $n+1$ 连在一起就是直接算，否则就通过旋转来考虑。

使用计数题的常用方法：枚举一个最小的旋转角度来算，然后乘上角度的贡献，我们得到

然后把两个答案加起来就做完啦！使用分治 $\texttt{FFT}$ 即可达到 $O(n\log^2n)$ 的优秀复杂度。

当然，神仙们可以用 $\texttt{Berlekamp-Massey}$ 来做，就是把前面几项算出之后代入就好了。别叫我，我不会

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
using namespace std;
typedef int ll;
typedef long long int li;
const ll MAXN=262151,MOD=998244353,G=3,INVG=332748118;
ll x,res,cnt=1,limit=-1;
ll g[MAXN],g0[MAXN],g1[MAXN],g2[MAXN],f0[MAXN],rev[MAXN];
ll f1[MAXN],f2[MAXN],tmp1[MAXN],tmp2[MAXN],tmp3[MAXN],tmp4[MAXN];
ll p0[MAXN],p1[MAXN],tmpg0[MAXN],tmpg1[MAXN],tmpg2[MAXN];
inline ll read()
{
    register ll num=0,neg=1;
    register char ch=getchar();
    while(!isdigit(ch)&&ch!='-')
    {
        ch=getchar();
    }
    if(ch=='-')
    {
        neg=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        num=(num<<3)+(num<<1)+(ch-'0');
        ch=getchar();
    }
    return num*neg;
}
inline ll qpow(ll base,ll exponent)
{
    li res=1;
    while(exponent)
    {
        if(exponent&1)
        {
            res=(li)res*base%MOD;
        }
        base=(li)base*base%MOD,exponent>>=1;
    }
    return res;
}
inline void NTT(ll *cp,ll cnt,ll inv)
{
    ll cur=0,res=0,omg=0;
    for(register int i=0;i<cnt;i++)
    {
        if(i<rev[i])
        {
            swap(cp[i],cp[rev[i]]);
        }
    }
    for(register int i=2;i<=cnt;i<<=1)
    {
        cur=i>>1,res=qpow(inv==1?G:INVG,(MOD-1)/i);
        for(register ll *p=cp;p!=cp+cnt;p+=i)
        {
            omg=1;
            for(register int j=0;j<cur;j++)
            {
                ll t=(li)omg*p[j+cur]%MOD,t2=p[j];
                p[j+cur]=(t2-t+MOD)%MOD,p[j]=(t2+t)%MOD;
                omg=(li)omg*res%MOD;
            }
        }
    }
    if(inv==-1)
    {
        ll invl=qpow(cnt,MOD-2);
        for(register int i=0;i<=cnt;i++)
        {
            cp[i]=(li)cp[i]*invl%MOD;
        }
    }
}
inline void calc(ll l,ll r)
{
	ll cnt=1,limit=-1,mid=(l+r)>>1;
	while(cnt<=(r-l+1)<<1)
	{
		cnt<<=1,limit++;
	}
	for(register int i=0;i<cnt>>1;i++)
	{
		p0[i]=i+l<=mid?f0[i+l]:0,p1[i]=i+l<=mid?f1[i+l]:0;
		tmpg0[i]=g0[i],tmpg1[i]=g1[i],tmpg2[i]=g2[i];
		rev[i]=(rev[i>>1]>>1)|((i&1)<<limit);
	}
	for(register int i=cnt>>1;i<cnt;i++)
	{
		tmpg0[i]=tmpg1[i]=tmpg2[i]=p0[i]=p1[i]=0;
		rev[i]=(rev[i>>1]>>1)|((i&1)<<limit);
	}
	NTT(tmpg0,cnt,1),NTT(tmpg1,cnt,1),NTT(tmpg2,cnt,1);
	NTT(p0,cnt,1),NTT(p1,cnt,1);
	for(register int i=0;i<cnt;i++)
	{
		tmp1[i]=(li)tmpg0[i]*p0[i]%MOD,tmp2[i]=(li)tmpg1[i]*p0[i]%MOD;
		tmp3[i]=(li)tmpg1[i]*p1[i]%MOD,tmp4[i]=(li)tmpg2[i]*p1[i]%MOD;
		tmpg0[i]=tmpg1[i]=tmpg2[i]=p0[i]=p1[i]=0;
	}
	NTT(tmp1,cnt,-1),NTT(tmp2,cnt,-1),NTT(tmp3,cnt,-1),NTT(tmp4,cnt,-1);
	for(register int i=0;i<cnt>>1;i++)
	{
		if(i+l>=mid&&i+l<r)
		{
			f0[i+l+1]=(f0[i+l+1]+tmp1[i])%MOD;
			f1[i+l+1]=(f1[i+l+1]+tmp2[i])%MOD;
		}
		if(i+l>=mid-2&&i+l<r-2)
		{
			f0[i+l+3]=(f0[i+l+3]+tmp3[i])%MOD;
			f1[i+l+3]=(f1[i+l+3]+tmp4[i])%MOD;
		}
	}
}
inline void cdqFFT(ll l,ll r)
{
	if(l==r)
	{
		f0[l]=(f0[l]+g0[l])%MOD,f1[l]=(f1[l]+g1[l])%MOD;
		return;
	}
	ll mid=(l+r)>>1;
	cdqFFT(l,mid),calc(l,r),cdqFFT(mid+1,r);
}
inline void calc2(ll l,ll r)
{
	ll cnt=1,limit=-1,mid=(l+r)>>1;
	while(cnt<=(r-l+1)<<1)
	{
		cnt<<=1,limit++;
	}
	for(register int i=0;i<cnt>>1;i++)
	{
		p0[i]=i+l<=mid?f2[i+l]:0,tmpg2[i]=g2[i],tmp2[i]=0;
		rev[i]=(rev[i>>1]>>1)|((i&1)<<limit);
	}
	for(register int i=cnt>>1;i<cnt;i++)
	{
		p0[i]=tmpg2[i]=tmp2[i]=0;
		rev[i]=(rev[i>>1]>>1)|((i&1)<<limit);
	}
	NTT(p0,cnt,1),NTT(tmpg2,cnt,1);
	for(register int i=0;i<cnt;i++)
	{
		tmp2[i]=(li)p0[i]*tmpg2[i]%MOD,p0[i]=tmpg2[i]=0;
	}
	NTT(tmp2,cnt,-1);
	for(register int i=0;i<cnt>>1;i++)
	{
		if(i+l>=mid-2&&i+l<r-2)
		{
			f2[i+l+3]=(li)(f2[i+l+3]+tmp2[i])%MOD;
		}
	}
}
inline void cdqFFT2(ll l,ll r)
{
	if(l==r)
	{
		f2[l]=((f2[l]+g2[l])%MOD+(l>=1?tmp1[l-1]:0))%MOD;
		return;
	}
	ll mid=(l+r)>>1;
	cdqFFT2(l,mid),calc2(l,r),cdqFFT2(mid+1,r);
}
int main()
{
	x=read(),g[0]=g[2]=1;
	for(register int i=4;i<=x;i+=2)
	{
		g[i]=(g[i-4]+g[i-2])%MOD;
	}
	for(register int i=0;i<=x;i++)
	{
		g0[i]=(li)g[i]*i%MOD*i%MOD,g1[i]=(li)g[i]*(i+1)%MOD*(i+1)%MOD;
		g2[i]=(li)g[i]*(i+2)%MOD*(i+2)%MOD;
	}
	cdqFFT(0,x);
	while(cnt<=(x<<1))
	{
		cnt<<=1,limit++;
	}
	for(register int i=0;i<cnt;i++)
	{
		rev[i]=(rev[i>>1]>>1)|((i&1)<<limit);
		tmpg0[i]=i<cnt>>1?f1[i]:0,tmpg1[i]=i<cnt>>1?g1[i]:0,tmp1[i]=0;
	}
	NTT(tmpg0,cnt,1),NTT(tmpg1,cnt,1);
	for(register int i=0;i<cnt;i++)
	{
		tmp1[i]=(li)tmpg0[i]*tmpg1[i]%MOD,tmpg0[i]=tmpg1[i]=0;
	}
	NTT(tmp1,cnt,-1),cdqFFT2(0,x);
	res=(li)(g[x-1]+g[x-3])*(x-1)%MOD*(x-1)%MOD*x%MOD;
	for(register int i=2;i<x-1;i++)
	{
		res=(res+(li)g0[i-1]*f0[x-i-1]%MOD*i%MOD)%MOD;
		res=(res+(li)g1[i-2]*f1[x-i-2]%MOD*2%MOD*i%MOD)%MOD;
		if(i>2&&i<x-2)
		{
			res=(res+(li)g2[i-3]*f2[x-i-3]%MOD*i%MOD)%MOD;
		}
	}
	printf("%d\n",res);
}